折板屋根の塗装面積を正確に求めるには❓形状により係数が異なる

「屋根塗り替えの見積書がきたけど、塗装面積が違うような気がする」

 

屋根の塗装工事では、実際に塗装する面積を求めるのは大事な作業です。
一般的な屋根の面積の求め方については、別記事で解説していましたね。

 

ただし特殊な形状の屋根については、この計算方法だけでは面積は求められません。
特に折れ曲がった形状の折板屋根を塗装するときは、慣れない業者だと見積書が間違っていることも多いですね。
今回はそんな折板屋根の塗装面積を求める方法について、図解しながら解説していきます。

 

 

 

平らなスレート屋根の場合、塗装面積は屋根（の投影）面積と同じなので、比較的計算が単純です。

 

しかし折板屋根の場合は、折れ曲がった部分があるので塗装面積＞屋根面積となりますね。
その塗装面積を求めるには、まず折板屋根の形状に応じた係数を求める必要があります。
実際に例をあげながら計算してみましょう。

塗装面積の計算を流れに沿って説明していきましょう。

 

妻側の長さを求める

今回の例では切妻屋根なので、斜辺の長さを求めなければいけません。
直角三角形の斜辺の長さは、短辺²＋長辺²＝斜辺²の式を利用して求められますね。

 

棟側の長さを求める

この棟側の長さを求めるときに、折板屋根独特の係数を考える必要があります。

図のように、折板屋根はジグザグ部分の長さがあります。
だから見た目の長さよりも余計に見込んでいく必要があるのですね。

 

ヨドルーフ88という折板屋根を例に計算してみましょう。

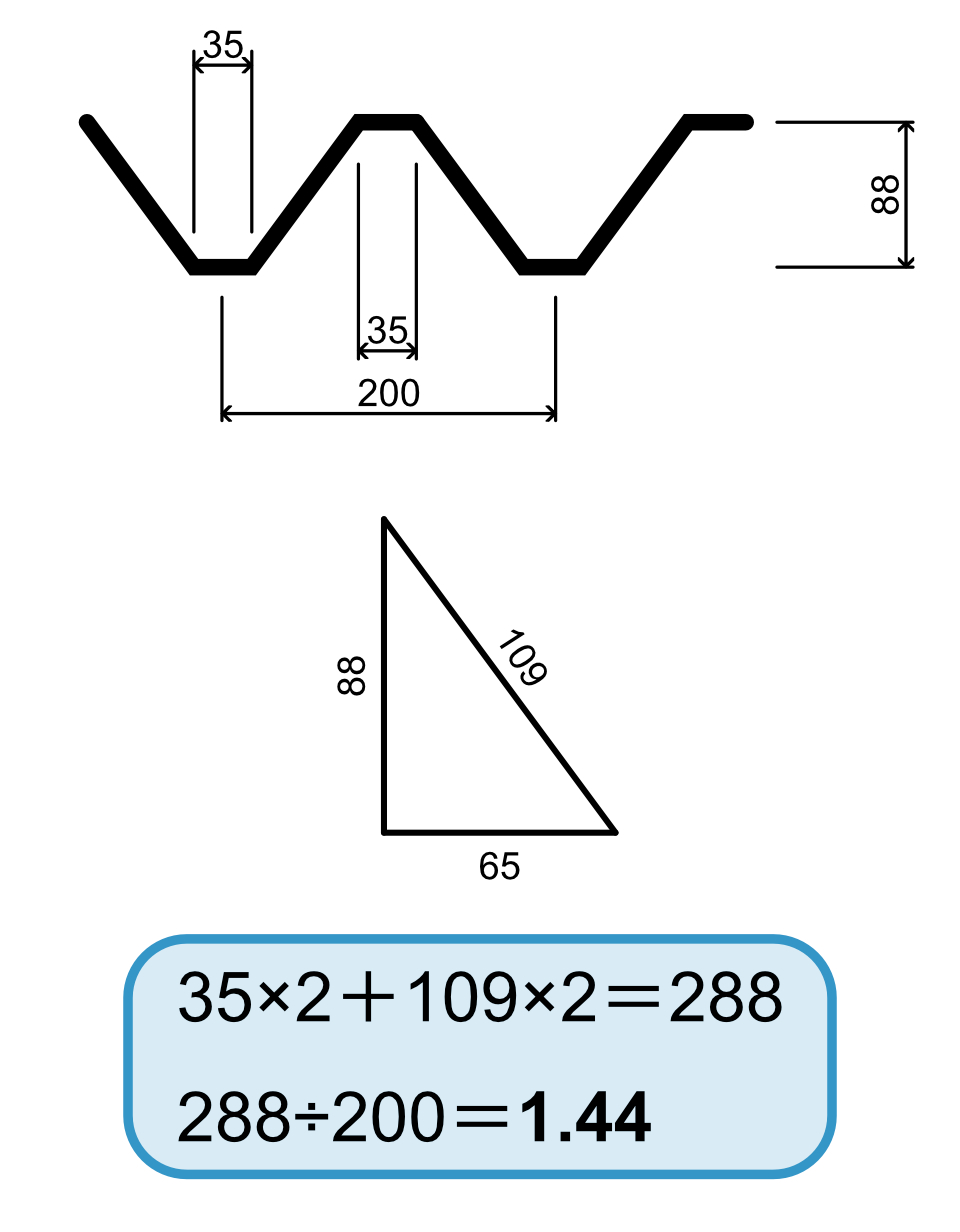
ヨドルーフ88では、一山の距離（ピッチ）が200mmです。
そして一山の中に斜辺が2つありますから、その長さを求めてあげます。
そして直線部分も加えた長さが288mm。
ピッチ長200mmで除してあげると、係数1.44が出てきますね。

 

この係数を棟側長さにかければ、塗装長さが算出できます。

 

塗装面積を求める

妻側長さ×棟側長さ×2で、今回の塗装面積を求めます。

今回はヨドルーフ88を例にとって計算しましたが、折板屋根の形状が異なれば係数も変わります。
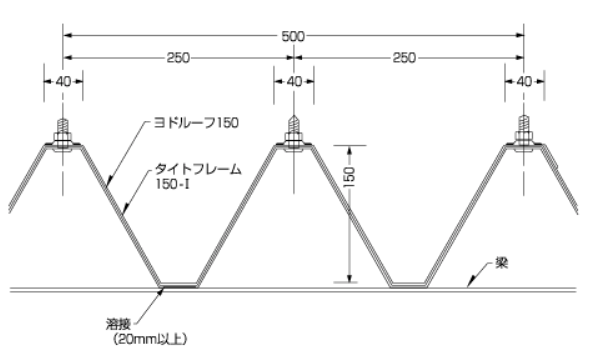
例えばヨドルーフ150となると、係数の計算は以下の通り。

係数が1.7となりました。
この係数を使って先ほどの屋根の塗装面積を計算してみると、以下の通り。

1,101.6㎡＞933.12㎡という差が出てきましたね。

 

したがって折板屋根を塗装工事するときは、見積り段階で屋根の形状に熟知した専門業者に依頼しなければいけません。
屋根工事に精通した業者を見つけるには、インターネット経由の一括見積もりサイトが便利です。
あなたの地域で信頼できる業者が見つかりますよ。